Accès aux éléments
On accède aux éléments d'un ndarray avec une notation similaire à celle utilisée avec les listes Python. On peut accéder à un élément à un indice particulier, extraire un sous-tableau ou itérer sur les éléments.
Indexation
Pour accéder à un élément d'un tableau, il suffit d'utiliser l'opérateur d'accès [] et d'indiquer la position de l'élément désiré, sur chacun des axes. Voici un exemple avec un tableau à trois dimensions :
On cherche donc l'élément qui est en deuxième position (indice $1$) sur le premier axe, également en deuxième position (indice $1$) sur le deuxième axe et enfin en première position sur le troisième et dernier axe. Ce dernier vaut $4$ comme en témoigne le résultat de l'exécution :
[[[1] [2]] [[3] [4]]] 4
Pour accéder à un élément précis d'un tableau multidimensionnel, on est obligé de préciser un indice pour chacune de ses dimensions. On peut ne pas donner d'indice pour toutes les dimensions, dans lequel cas, on obtiendra comme résultat un sous-tableau et non pas un élément précis. Voici deux exemples d'accès à un sous-tableau :
La première instruction extrait le premier élément de la première dimension du tableau data, à savoir un sous-tableau de dimension $(2, 1)$ qui contient les éléments $1$ et $2$. La seconde instruction extrait le second élément du second élément du tableau data, à savoir un sous-tableau de dimension $(1,)$ qui contient uniquement l'élément $4$ :
[[1] [2]] [4]
Tout comme avec les listes Python, on peut également utiliser un indice négatif, si on veut compter à partir de la fin. Voici comment récupérer l'élément qui est le dernier dans chacune des dimensions :
On obtient le même résultat qu'avec data[1,1,0], à savoir $4$. C'est logique puisque les dimensions du tableau data sont $(2, 2, 1)$ et que la séquence d'indices $(1,1,0)$ identifie donc son « dernier » élément.
Slicing
On a vu plus haut qu'il est possible d'extraire un sous-tableau à partir d'un ndarray, en utilisant l'opérateur d'accès et en ne spécifiant pas un indice pour toutes les dimensions. Avec cette technique, on est limité puisqu'on ne pourrait pas, par exemple, uniquement spécifier un indice pour la dernière dimension, et rien pour les autres.
Une autre technique consiste à utiliser l'opérateur de slicing, comme celui disponible pour les listes Python, pour sélectionner plusieurs éléments sur une ou plusieurs dimensions du tableau. Commençons par un exemple sur un tableau unidimensionnel :
Le premier sous-tableau extrait de data est le sous-tableau commençant à l'indice $2$ (inclus) et se terminant à l'indice $4$ (exclu). On peut ne pas préciser l'indice de fin, dans lequel cas le sous-tableau s'étend jusqu'au bout du tableau original. De même, si on ne précise pas l'indice de début, le sous-tableau commence au début du tableau original. Enfin, si on ne précise aucun des deux indices, on récupère tout le tableau original. Voici les quatre sous-tableaux extraits par l'exemple :
[2 3] [3 4 5 6 7 8] [0 1 2] [0 1 2 3 4 5 6 7 8]
La figure 4 montre le tableau original data avec les quatre sous-tableaux extraits. On y voit bien que l'indice de fin est toujours exclu.
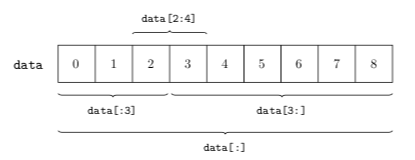
ndarray en précisant les indices de début (inclus) et de fin (exclu) du sous-tableau à extraire.La forme générale qui permet de décrire un sous-tableau est en fait start:end:step. En effet, on peut définir un pas d'incrément et du coup ne pas forcément prendre des éléments consécutifs dans le sous-tableau extrait. S'il n'est pas précisé, la valeur par défaut de step est $1$. Voici un exemple sur base du tableau précédent :
Comme on n'a rien spécifié pour start et end, on part de tout le tableau, mais comme on a spécifié un pas d'incrément de $2$, on ne gardera qu'un seul élément sur deux dans le sous-tableau extrait :
[0 2 4 6 8]
On peut également spécifier un pas d'incrément négatif, dans lequel cas le « parcours » fait pour extraire les éléments du sous-tableau commence par la fin. Voici un exemple avec un pas d'incrément négatif :
On se retrouve avec un tableau qui possède exactement les mêmes dimensions, mais dont l'ordre des valeurs a été modifié :
[8 7 6 5 4 3 2 1 0]
Tableau multidimensionnel
On peut évidemment utiliser l'opérateur de slicing pour des tableaux à plus d'une dimension. L'exemple suivant déclare un tableau à deux dimensions et en extrait des sous-tableaux :
La première instruction extrait un sous-tableau qui va contenir tous les éléments d'indices $1$ (inclus) à $3$ (exclu) dans la première dimension, et d'indices $1$ (inclus) à $4$ (exclu) dans la seconde.
Autrement dit, on prend le sous-tableau de deux « lignes » et de trois « colonnes » qui se situe « en bas à droite » de data. Les deux autres instructions extraient respectivement la première « ligne » et la première « colonne » de data.
Comme on peut voir sur le résultat de l'exécution, la première « colonne » extraite par data[:,0] est renvoyée sous la forme d'une « ligne », c'est-à-dire un tableau unidimensionnel :
[[ 5 6 7] [ 9 10 11]] [0 1 2 3] [0 4 8]
La figure 5 montre visuellement à quoi correspondent les sous-tableaux extraits du tableau data. Lorsque l'on analyse des tableaux à deux dimensions, la visualisation est assez immédiate, et un sous-tableau produit par l'opérateur de slicing avec des pas d'incrément de $1$ correspond toujours à un « rectangle ». On peut évidemment utiliser l'opérateur de slicing avec des tableaux qui ont plus de deux dimensions.
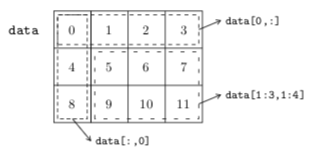
ndarray à deux dimensions en précisant les indices de début (inclus) et de fin (exclu) du sous-tableau à extraire, pour chacune des deux dimensions.Revenons un moment sur l'observation que l'on a faite sur le résultat de l'opération data[:,0]. La raison pour laquelle on s'est retrouvé avec une « ligne » et non pas une « colonne » comme résultat est simplement que lorsque l'on n'utilise qu'une seule valeur comme indice pour un axe, la dimension correspondante est réduite de un. Dans notre cas, on passe donc de deux dimensions à une dimension.
Si on avait écrit data[:,0:1] à la place, on aurait obtenu les mêmes éléments, mais sous la forme d'une « colonne », car l'indice n'est plus une simple valeur, mais un slice :
[[0] [4] [8]]
Liste d'indices
La définition d'un slice permet donc de sélectionner des éléments qui se suivent dans une dimension, ou qui sont espacés d'une même distance si on spécifie un pas d'incrément. On peut faire une sélection plus complexe en spécifiant une liste d'indices à extraire, pour chacune des dimensions. En repartant du tableau data de l'exemple précédent, on peut, par exemple, écrire l'instruction suivante :
Dans la première dimension, on sélectionne la première « ligne » (avec 0:1) et dans la seconde dimension, on sélectionne trois « colonnes », celles dont les indices sont $0$, $2$ et $3$ (avec [0, 2, 3]). Le résultat de l'exécution est le sous-tableau de dimensions $(1, 3)$ suivant :
[[0 2 3]]
On peut évidemment spécifier des listes d'indices pour toutes les dimensions. Si ces listes sont de mêmes tailles, on va en fait cibler un ensemble précis d'éléments. Voici, par exemple, comment extraire les éléments dont les « coordonnées » sont $(0, 0)$, $(1, 3)$ et $(2, 1)$ :
Les trois éléments ciblés par cet accès sont renvoyés ensemble sous la forme d'une unique liste unidimensionnelle :
[0 7 9]
Modification
Une fois que l'on sait accéder à un élément ou à un sous-tableau d'un tableau multidimensionnel, on peut également le modifier en utilisant l'opérateur [] à gauche de l'instruction d'affectation. Il faut évidemment que le nombre d'éléments et que les dimensions correspondent pour que la modification ne produise pas d'erreur. Les instructions suivantes déclarent un tableau à deux dimensions et modifient ensuite un des éléments de ce tableau :
On voit bien sur le résultat de l'exécution que l'élément à l'indice $1$ de la première dimension et à l'indice $0$ de la seconde a été modifié :
[[0 1 2] [3 4 5]] [[ 0 1 2] [-1 4 5]]
On peut aussi modifier les éléments d'un sous-tableau, pour autant que l'on fournisse le bon nombre d'éléments et qu'ils soient sous la forme d'un tableau avec les bonnes dimensions. L'exemple suivant modifie la dernière « colonne » du tableau data :
On sélectionne donc toutes les « lignes » du tableau à partir de la deuxième « colonne » et on remplace le sous-tableau correspondant par un tableau rempli de $-2$, de dimensions $(2, 1)$. On voit donc que tous les éléments de la dernière « colonne » ont été changés en $-2$ :
[[ 0 1 -2] [-1 4 -2]]
Si le nombre de valeurs ou les dimensions ne sont pas corrects, une erreur d'exécution se produit lors de l'exécution.
Vue et copie
Toutes les opérations de slicing simple vues plus haut construisent un nouvel objet ndarray, mais il n'y a jamais de copie des éléments. Le nouvel objet est une vue du tableau original et une modification d'un élément depuis un sous-tableau construit par slicing sera donc également appliquée sur le tableau original. Voici un exemple illustrant cela :
La deuxième instruction extrait un sous-tableau de data que l'on stocke dans la variable new. On modifie ensuite le premier élément de ce sous-tableau et, comme on le voit sur le résultat de l'exécution, le tableau original est également modifié :
[12 3 4 5] [ 0 1 12 3 4 5 6 7 8]
La raison pour laquelle NumPy préfère calculer des vues, lorsque c'est possible, est simplement que cela économise de la mémoire. Si vous voulez être sûr d'avoir une copie, et non pas une vue, il suffit d'appeler la méthode copy des objets ndarray. Voici ce que devient la deuxième instruction de l'exemple précédent :
Si l'on exécute le programme avec ce changement, on constate que l'on a bel et bien une copie du tableau original puisque ce dernier n'est, cette fois-ci, pas modifié suite à la modification sur new :
[12 3 4 5] [0 1 2 3 4 5 6 7 8]
Il n'est pas toujours aisé de se rappeler, pour chaque opération, fonction ou méthode, si elles produisent une vue ou une copie du tableau sur lequel elles opèrent. Idéalement, on ne devrait jamais se poser de questions et laisser faire le comportement par défaut, sauf si on doit modifier le tableau produit et que l'on veut être certain de laisser le tableau original inchangé. Dans ce cas, la copie est nécessaire et, outre la méthode copy des objets ndarray, on peut également utiliser la fonction copy de NumPy ou utiliser le paramètre optionnel copy de la fonction array comme l'illustre l'exemple suivant :
Les variables a et b contiennent chacune une copie du tableau data dont les valeurs des éléments sont inchangées, suite aux modifications faites sur les copies, comme on le voit sur le résultat de l'exécution :
[0 1 2] [12 1 2] [99 1 2]
Un défaut des copies est que la consommation mémoire de votre programme sera plus grande et que les performances seront un peu diminuées, cela prend en effet un peu de temps pour réaliser des copies.
Itération
Le dernier type d'accès que l'on peut faire sur un ndarray consiste à parcourir ses éléments. La méthode la plus directe pour ce faire consiste à naviguer dans le tableau en parcourant tous les indices possibles des différents axes. Voici un exemple avec un tableau à trois dimensions :
On commence par extraire le nombre d'éléments de chacune des dimensions du tableau dans trois variables x, y et z. On parcourt ensuite le tableau avec trois boucles for imbriquées et trois variables i, j et k qui parcourent toutes les valeurs possibles pour les indices, selon les trois axes du tableau parcouru. Enfin, on affiche chacun des éléments du tableau en les récupérant à l'aide de l'opérateur d'accès. Le résultat affiche donc tous les éléments du tableau :
0 1 2 3 4 5
Si on n'a pas besoin de connaitre les indices, mais que l'on veut simplement parcourir les éléments du tableau, on peut directement utiliser un itérateur sur le tableau. Ce dernier permet d'itérer sur les éléments de la première dimension du tableau parcouru. Voici une telle boucle, sur le même tableau que l'exemple précédent :
Dans notre cas, la boucle ne se répète qu'une seule fois, puisqu'il n'y a qu'un seul élément dans la première dimension. Le résultat de l'exécution confirme ceci, tout le tableau s'affichant en une seule fois :
[[0 1 2] [3 4 5]]
Pour parcourir tous les éléments, comme on l'a fait avec les indices, il faut donc de nouveau utiliser trois boucles imbriquées :
Enfin, si on veut parcourir tous les éléments d'un tableau, mais que l'on n'a pas besoin d'information par rapport aux dimensions, on peut passer par l'attribut flat qui donne directement un itérateur sur les éléments. Les exemples précédents peuvent se réécrire comme suit :
L'attribut flat construit en fait un itérateur sur une vue aplatie du tableau, c'est-à-dire une vue unidimensionnelle avec ses éléments pris en suivant un parcours « naturel ». On a déjà pu voir une telle construction à la section 2.2.3 où on pouvait faire des combinaisons de tableau aplatis en utilisant le paramètre optionnel axis=None. La section 2.6 détaille comment on peut explicitement construire de telles vues.