Opération
Terminons ce chapitre sur les tableaux multidimensionnels en voyant comment on peut réaliser des opérations combinant des tableaux et des scalaires. On a déjà pu voir un aperçu des possibilités qu'offre NumPy à la section 2.2.1 lorsque l'on a vu comment initialiser un tableau avec une valeur $k$. On pouvait, par exemple, créer un tableau initialisé avec des $1$ avec la fonction ones et ensuite multiplier tous ses éléments par $k$.
Opération élément par élément
La première catégorie d'opérations que l'on peut réaliser reprend les opérations arithmétiques binaires, c'est-à-dire ceux qui prennent deux opérandes. Elles se font entre deux tableaux compatibles, c'est-à-dire avec la même taille et la même forme, et élément par élément. Examinons l'exemple de programme suivant :
Les premières instructions créent deux tableaux de forme $(2, 2)$, stockés dans les variables a et b. On calcule ensuite la somme de ces deux tableaux et on stocke le résultat dans la variable data. Les éléments de a et b situés à la même position sont additionnés pour produire les différents éléments du résultat. Comme on le voit sur le résultat de l'exécution, on a donc ajouté $1$ à tous les éléments de a :
[[ 1 -1] [ 2 3]] [[0 1] [2 3]] [[1 0] [4 6]]
La figure 8 illustre le calcul qui est réalisé. On y voit clairement que les différents éléments des deux tableaux additionnés le sont un à un. On peut aussi faire des soustractions (-), des multiplications (*), des divisions entières (//) ou flottantes (/) et des exponentiations (**).
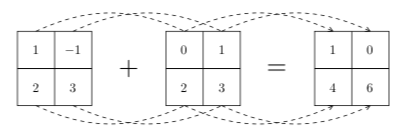
ndarray de mêmes tailles et de mêmes dimensions construit un résultat de même taille et dimensions dont les éléments sont la somme des éléments placés aux mêmes positions dans les tableaux à additionner.Concernant les divisions, un avertissement de type RuntimeWarning s'affiche lorsque le diviseur est nul, le résultat étant $\infty$ pour la division flottante et $0$ pour la division entière. Voici, par exemple, le résultat de l'exécution si on remplace la somme par une division entière :
[[ 1 -1] [ 2 3]] [[0 1] [2 3]] program.py:8: RuntimeWarning: divide by zero encountered in floor_divide data = a // b [[ 0 -1] [ 1 1]]
Pour changer ce comportement par défaut, il suffit d'utiliser la fonction seterr qui permet de décider ce qu'on veut faire en cas d'avertissement, pour les différents types possibles, comme l'ignorer (ignore) ou lever une exception (raise), par exemple. Pour ignorer tous les avertissements, mais lever une exception pour les erreurs de division, il suffit de commencer le programme par :
On se retrouve donc maintenant avec l'erreur suivante, que l'on peut évidemment éviter en ajoutant un try/except :
Traceback (most recent call last): File "program.py", line 9, indata = a // b FloatingPointError: divide by zero encountered in floor_divide
Performance
Lorsque l'on désire faire une opération sur les éléments d'un tableau, pour en modifier les valeurs, on peut utiliser la forme compacte des opérateurs arithmétiques. Pour comprendre, commençons par analyser ce que fait l'exemple suivant :
Ces instructions calculent les puissances de $2$, en commençant par $2^2$ pour finir avec $2^{10}$. On construit d'abord un tableau unidimensionnel avec $10$ éléments initialisés à deux, et on le multiplie par une séquence incrémentale allant de $1$ à $10$ (inclus). On se retrouve ainsi avec le résultat désiré dans data :
[[ 2 4 8 16 32 64 128 256 512 1024]]
Puisque l'on stocke le résultat de l'opération directement dans l'un des deux opérandes, il est plus efficace d'utiliser la notation compacte, pour éviter que NumPy ne crée un nouveau tableau, le cas échéant. Pour notre exemple, il est donc plus efficace d'écrire :
Fonction prédéfinie
Une autre type d'opérations que l'on peut réaliser est représenté par des fonctions prédéfinies. Ces dernières opèrent sur un tableau et en produise un de même taille et de même forme. On retrouve toutes les fonctions classiques : trigonométriques, racines, exponentielles, logarithmes, etc.
L'exemple suivant permet de vérifier l'identité $\sin^2(x) + \cos^2(x) = 1$, pour plusieurs valeurs possibles de $x$ :
La fonction isclose permet de tester qu'une valeur qui est un nombre flottant est proche d'une valeur spécifiée. En effet, les calculs en nombres flottants n'ont pas toujours une grande précision et tester une égalité exacte est souvent impossible. On se retrouve évidemment avec un tableau ne contenant que des True comme résultat :
[ True True True True True True True True True True]
Expression vectorielle
Parfois, ce que l'on désire faire, c'est appliquer la même opération à tous les éléments d'un même tableau. En Python, on ferait cela à l'aide d'une boucle qui parcourt tout le tableau et applique l'opération sur chacun de ses éléments. En NumPy, on utilise une expression vectorielle qui correspond généralement à une combinaison d'un tableau avec un scalaire, comme dans l'exemple suivant :
On commence par créer un tableau bidimensionnel avec six éléments, construit sur base d'une séquence incrémentale. On construit ensuite deux nouveaux tableaux que l'on affiche directement. Dans le premier cas, on ajoute 1j à chaque élément, créant ainsi un tableau de complexes. Dans le second cas, on élève au carré chaque élément. Il s'agit à chaque fois de nouveaux tableaux, l'original data n'étant pas modifié :
[[0.+1.j 1.+1.j 2.+1.j] [3.+1.j 4.+1.j 5.+1.j]] [[ 0 1 4] [ 9 16 25]] [[0 1 2] [3 4 5]]
Cette possibilité de construire des expressions vectorielles, offerte par NumPy, permet de réaliser des opérations en masse sans utiliser explicitement de boucles et en gardant ainsi un code lisible. En fait, pour comprendre ce qui se passe, il suffit d'imaginer que le scalaire a été utilisé pour initialiser un tableau de même taille et de même forme. La seconde opération, à savoir data ** 2, correspond en fait à l'opération élément par élément suivante :
La figure 9 montre l'opération élément par élément à laquelle correspond l'expression vectorielle data ** 2. Il ne s'agit évidemment que d'un équivalent pour comprendre ce qui se passe, l'expression vectorielle étant à favoriser puisqu'elle optimise l'occupation mémoire.

On peut évidemment construire des expressions vectorielles plus complexes, qui combinent les deux types d'opérations. Par exemple, on pourrait vouloir évaluer le polynôme $3x^2 - 5x + 1$ pour plusieurs valeurs de $x$. Pour cela, on peut simplement écrire :
Broadcasting
On peut en fait aller encore plus loin concernant les opérations entre deux tableaux. En réalité, de telles opérations sont possibles si l'un des deux tableaux peut être broadcasté sur l'autre. Pour comprendre ce que cela signifie, partons de l'exemple suivant :
Dans cet exemple, on tente donc de faire la somme entre un tableau de dimensions $(3, 3)$ avec un tableau de dimensions $(1, 3)$. De prime abord, les tableaux n'étant pas compatibles, on pourrait penser que cela produira une erreur lors de l'exécution. Néanmoins, ce code fonctionne sans erreur et produit un tableau de dimensions $(3, 3)$ comme résultat.
L'exécution produit le tableau suivant comme résultat :
[[10 11 12] [10 11 12] [10 11 12]]
Pour comprendre, c'est en fait comme si le tableau a avait été empilé verticalement trois fois, pour en faire un tableau de dimensions $(3, 3)$ qui puisse ensuite être additionné à data. La figure 10 illustre à quoi correspond le calcul qui s'est produit.
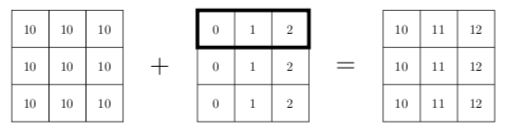
Pour encore mieux comprendre ce qui se passe, il suffit d'imaginer que le tableau a a été empilé trois fois verticalement avant de l'additionner à data. L'opération data + a correspond donc en fait à :
Pour résumer, si on fait une opération entre un scalaire et un tableau, l'opération est « simultanément » exécutée entre le scalaire et chacun des éléments du tableau. Si on fait une opération entre deux tableaux, les règles sont un peu différentes :
- Soit les deux tableaux ont exactement la même taille et la même forme, dans lequel cas l'opération se fait entre les éléments situés à la même position afin de produire le résultat qui sera un tableau de même taille et de même forme.
- Sinon, il faut que l'un des deux tableaux puisse être broadcasté sur l'autre, c'est-à-dire que pour chaque axe, on a soit le même nombre d'éléments dans les deux tableaux, soit $1$ pour l'un des deux tableaux. Un tableau de dimensions $(1, 3)$ peut, par exemple, être broadcasté sur un tableau de dimensions $(3, 3)$ comme ce qui s'est passé dans l'exemple précédent.
La manière avec laquelle un tableau est broadcasté sur un autre dépend des dimensions. Dans l'exemple précédent, on a vu qu'il s'agissait en fait d'un empilement vertical. L'exemple suivant, illustré par la figure 11, fait la somme entre un tableau de dimensions $(3, 3)$ et un second tableau de dimensions $(3, 1)$. Cela revient à faire la somme entre data et le tableau a empilé trois fois, horizontalement cette fois-ci :
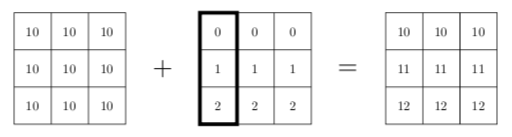
Vectorisation de fonction
Le broadcasting qui est réalisé par NumPy, pour la plupart des opérations, permet d'obtenir un gain de temps d'exécution non négligeable. En effet, plusieurs opérations peuvent être effectivement exécutées en parallèle, grâce à cette propriété.
Il est possible de profiter de cette possibilité, de calcul vectoriel, pour les fonctions que l'on définit soi-même. Pour voir comment cela fonctionne, partons de l'exemple suivant qui définit une fonction ticket_price qui calcule le prix d'un ticket en fonction de l'âge d'une personne :
Si l'on souhaite appeler cette fonction avec un ndarray, pour trouver le prix des tickets pour plusieurs personnes, on est obligé de faire explicitement une boucle qui va parcourir le tableau et appeler la fonction pour chacun de ses éléments. On reconstruit ensuite un nouveau tableau avec les résultats de ces appels. En utilisant une définition par compréhension, on peut écrire :
Le résultat de l'exécution produit bel et bien un ndarray unidimensionnel avec neuf éléments représentant les prix des tickets :
[ 0 0 0 10 10 10 15 10 10]
Grâce à la fonction vectorize, on va pouvoir automatiquement transformer une fonction pour faire en sorte qu'elle puisse prendre en paramètre un tableau et construire un tableau comme résultat. Elle permet en fait de vectoriser une fonction. On peut donc écrire :
La fonction vectorize renvoie donc une fonction que l'on peut ensuite utiliser avec des paramètres de type ndarray, ce qui permet d'avoir un code beaucoup plus propre. Parfois, on ne souhaite pas que tous les paramètres d'une fonction soient vectorisés. Dans ce cas, il suffit de déclarer la liste des paramètres à exclure. Voici, par exemple, une fonction qui permet d'évaluer la valeur d'un polynôme dont on donne la liste des coefficients :
Le paramètre optionnel excluded contient une liste de nombres entiers qui indiquent les positions des paramètres qu'il ne faut pas vectoriser. Dans cet exemple, seul le paramètre x est donc vectorisé, ce qui permet de calculer la valeur d'un polynôme pour plusieurs points à la fois. Comme on le voit sur le résultat de l'exécution, ces instructions calculent donc la valeur de $x^2 + 1$ pour $x$ allant de $0$ à $9$ (inclus) :
[ 1 3 9 19 33 51 73 99 129 163]
Fonction d'agrégation
Toutes les opérations examinées plus haut dans cette section calculent à chaque fois un tableau comme résultat. Découvrons maintenant les fonctions d'agrégation qui permettent d'obtenir une seule valeur simple comme résultat d'une opération sur un tableau. Par exemple, on peut vouloir faire la somme de tous les éléments d'un tableau :
La fonction sum prend donc un tableau en paramètre et renvoie comme résultat la somme de ses éléments. Dans notre cas, l'exécution produit la valeur $3$ comme résultat :
3
On aurait pu se passer de la fonction sum de NumPy et plutôt utiliser la fonction prédéfinie sum de Python appelée sur l'itérateur du tableau data obtenu avec l'attribut flat :
Le résultat produit est exactement le même, mais les performances sont bien meilleures avec la fonction sum de NumPy. Par exemple, pour faire la somme des éléments d'un np.arange(1e5), un tableau à 100000 éléments, il faut en moyenne 10,59 ms avec la fonction prédéfinie sum de Python contre 0,12 ms avec la version de NumPy.
Il est également possible de calculer plusieurs sommes à partir d'un tableau multidimensionnel, en suivant un ou des axes spécifiés. Pour un tableau à deux dimensions, on pourrait, par exemple, calculer les sommes des éléments de chaque « ligne » ou de chaque « colonne ». Dans ce cas, le résultat n'est plus une simple valeur, mais un tableau unidimensionnel, par défaut. Pour calculer de telles sommes, on utilise le paramètre optionnel axis :
La première instruction, avec axis=0, calcule les sommes des éléments de chaque « colonne » et la seconde avec axis=1 s'occupe des « lignes » :
[ 5 -2] [-1 4]
Comme on le voit sur le résultat de l'exécution, peu importe sur quel axe les sommes sont calculées, le résultat est toujours un tableau unidimensionnel. Si on veut conserver les dimensions, il faut utiliser le paramètre optionnel keepdims. Par exemple, pour la somme des éléments des lignes, on pourrait vouloir un tableau « colonne » comme résultat, comme illustré sur la figure 12. Pour ce faire, il suffit de remplacer la seconde instruction par la suivante :
Le résultat de l'exécution confirme qu'on obtient bien, cette fois-ci, un tableau de dimensions $(2, 1)$ comme résultat :
[[-1] [ 4]]
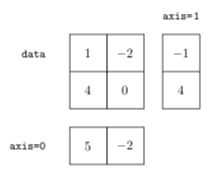
axis de la fonction sum permet de définir l'axe le long duquel les sommes doivent être calculées.On peut également faire la somme le long de plusieurs axes à la fois. Pour cela, il suffit de spécifier un tuple d'axes en paramètres. Pour notre exemple avec un tableau à deux dimensions, l'instruction suivante est en fait le comportement par défaut, à savoir le calcul de la somme de tous les éléments du tableau :
De nombreuses autres fonctions agrégatives existent, mais nous n'allons pas ici toutes les détailler. En vrac, on peut rechercher le minimum et le maximum d'un tableau (min et max), calculer le produit de ses éléments (prod) ou les sommes et produits cumulés (cumsum et cumprod) ou encore obtenir une série de statistiques de base comme la moyenne, la variance et l'écart-type (mean, var et std).
Il existe également des fonctions qui renvoient des booléens, telles que all et any. La première renvoie True si tous les éléments du tableau satisfont la condition et la seconde renvoie True si au moins un des éléments du tableau vaut True. On peut tester si des éléments du tableau data sont strictement positifs comme suit :
Tous les éléments de data n'étant pas strictement positifs, mais certains l'étant, la première instruction renvoie False et la seconde True :
False True
De nouveau, on peut spécifier l'axe (ou les axes) le long duquel on souhaite appliquer l'opération, à l'aide du paramètre optionnel axis.