Forme
En mémoire, un tableau multidimensionnel est donc toujours constitué d'une séquence de blocs consécutifs, peu importe ses dimensions du tableau, pour des questions de performance.
En plus des données stockées dans le tableau, NumPy retient d'autres informations sur ce dernier, notamment sa forme, accessible via l'attribut shape. Celui-ci contient le nombre d'éléments que chacune des dimensions du tableau contient et est déterminé à la création. L'exemple de code suivant crée trois ndarray et affiche leur forme :
Pour le premier tableau, on spécifie la forme explicitement à la création, à savoir $(3, 2, 1)$. Dans le deuxième cas, on utilise la fonction array en lui donnant une liste de listes en paramètres. Sa forme est $(2, 3)$ car le paramètre est une liste qui contient deux listes de trois éléments. Enfin, dans le dernier cas, la fonction arange construit un tableau unidimensionnel avec six éléments ce qui donne $(6,)$ comme forme. Voici le résultat de l'exécution qui confirme tout cela :
(3, 2, 1) (2, 3) (6,)
Modifier la forme
La forme d'un ndarray, bien qu'initialement déterminée à la création, n'est pas figée. On peut la modifier à l'aide de la fonction resize en précisant la nouvelle forme désirée, avec un seul paramètre de type tuple ou en listant simplement les dimensions désirées.
Voici un exemple de changement de forme d'un tableau unidimensionnel de forme $(6,)$, créé avec la fonction arange :
Le tableau data est créé avec une seule dimension et six éléments. Sa forme est ensuite modifiée et data se retrouve avec deux dimensions ayant respectivement deux et trois éléments :
(2, 3) [[0 1 2] [3 4 5]]
La fonction resize modifie donc le tableau sur lequel on l'applique. Cette opération est très rapide vu que les données n'ont pas été modifiées en mémoire, seule la manière de les interpréter a changé. Si on inspecte l'attribut strides, on voit que sa valeur est passée de $(8,)$ pour le tableau original à $(24, 8)$ après changement de forme. Les données du tableau après modification de forme n'ont donc pas changé.
Pour modifier la forme d'un tableau, mais sans modifier celle de l'original, il faut utiliser la fonction reshape. Cette dernière crée un nouveau tableau avec les mêmes données que le tableau original, mais avec une nouvelle forme. L'exemple suivant illustre cette fonction :
Comme on le voit sur le résultat de l'exécution, le tableau original n'a pas été modifié et a toujours une forme de $(6,)$. La fonction reshape construit un nouveau tableau, que l'on a stocké dans une variable new, avec les mêmes éléments que le tableau original, mais avec une autre forme, à savoir $(2, 3)$ dans notre exemple :
(6,) [0 1 2 3 4 5] (2, 3) [[0 1 2] [3 4 5]]
La fonction reshape construit en fait une nouvelle vue, comme le fait l'opérateur de slicing. Si on modifie les éléments du nouveau tableau, on peut donc voir les modifications sur le tableau original. On peut, par exemple, modifier la troisième « colonne » du tableau new en la remplaçant par un tableau de forme $(2, 1)$ initialisé avec des $-1$, créé avec la fonction full :
On voit bien sur le résultat de l'exécution que certains des éléments de data ont été modifiés, suite à la modification faite sur new. Cela confirme que la fonction reshape a bien construit une vue :
[ 0 1 -1 3 4 -1]
On peut laisser reshape calculer automatiquement le nombre d'éléments de certaines dimensions en spécifiant $-1$ au moment où l'on décrit la forme. On aurait donc pu écrire l'exemple précédent comme suit :
Notez que cette possibilité n'est pas utilisable avec la fonction resize, mais uniquement avec la fonction reshape. De plus, il ne peut y avoir qu'un seul $-1$ dans une description de forme, mais peu importe sa position. On peut, par exemple, écrire (1, -1, 3) ou (-1, 1, 1) comme nouvelle forme, mais pas (1, -1, -1). Dans le premier cas, le $-1$ est remplacé par $2$ et dans le second cas par $6$.
En réalité, les différences entre les fonctions resize et reshape sont bien plus complexes, comme on va voir plus loin dans le livre. Dans tous les cas, si vous voulez modifier la forme d'un tableau et être certain de ne pas modifier l'original si vous modifiez le nouveau, il est plus prudent d'appeler la fonction reshape suivie de copy. On aurait donc écrit :
Rétrécissement et agrandissement
Que se passe-t-il si la nouvelle forme fait que le tableau après modification comporte plus ou moins de données que l'original ? Si la nouvelle forme est plus petite, le tableau va subir un rétrécissement et perdre certains de ses éléments. Si la nouvelle forme est plus grande que celle de l'original, de nouveaux éléments, initialisés à la valeur $0$, sont ajoutés et on a un agrandissement. L'exemple suivant illustre ces deux possibilités :
Après un rétrécissement, les données retirées sont perdues à jamais. On le voit bien dans le résultat de l'exécution où les éléments $4$ et $5$, supprimés par le rétrécissement, ne sont pas revenus après agrandissement :
[0 1 2 3 4 5] [[0 1] [2 3]] [[0 1 2] [3 0 0]]
Le rétrécissement et l'agrandissement ne sont possibles qu'avec resize. Si vous tentez la même chose avec reshape, une erreur se produira si la nouvelle forme n'est pas compatible avec l'ancienne, c'est-à-dire que la nouvelle taille n'est pas la même que celle du tableau original.
Aplatissement
Enfin, un dernier type d'opération que l'on peut faire sur la forme d'un ndarray est l'aplatissement. Cette opération consiste à transformer un tableau multidimensionnel en un tableau à une seule dimension dont l'ordre des éléments est déterminé par un parcours du tableau à aplatir.
On peut réaliser cette opération avec la fonction ravel, qui renvoie donc un tableau unidimensionnel. Voici un exemple :
Dans cet exemple, la forme du tableau initialement créé est de $(2, 3)$ et le tableau aplati par ravel se retrouve avec une forme de $(6,)$. L'ordre dans lequel les éléments de data sont parcourus est l'ordre « naturel », c'est-à-dire celui produit par l'itérateur flat vu à la section 2.4.5. Voici le résultat de l'exécution qui montre le tableau aplati produit :
(6,) [1 2 3 4 5 6]
La fonction ravel calcule une vue, si possible, du tableau original. Elle peut ainsi être plus efficace et optimiser la mémoire utilisée. Modifier les éléments du tableau aplati créé peut donc aussi modifier les éléments du tableau original, comme l'illustre l'exemple suivant :
On a ici modifié le dernier élément du tableau aplati créé et on voit que la modification a aussi eu lieu sur le tableau original :
[ 1 2 3 4 5 -1] [[ 1 2 3] [ 4 5 -1]]
Il existe également la fonction flatten pour aplatir un tableau. La différence avec ravel est qu'elle crée toujours une copie du tableau à aplatir. Par conséquent, la fonction flatten est souvent plus lente, mais est plus sûre si vous voulez faire des modifications sur la version aplatie sans risquer de modifier le tableau original.
Enfin, autant avec ravel que flatten, on peut choisir l'ordre dans lequel les éléments sont parcourus pour construire l'aplatissement. Le comportement par défaut, c'est-à-dire le parcours « naturel » des éléments du tableau, revient généralement à exécuter un reshape(-1).
On peut choisir un autre ordre avec le paramètre optionnel order des fonctions ravel et flatten. Par défaut, le paramètre vaut 'C' pour faire un parcours comme dans le langage de programmation C, c'est-à-dire orienté « lignes ». On peut aussi faire un parcours comme en Fortran, c'est-à-dire orienté « colonnes », avec 'F'. Les deux autres possibilités, moins courantes, sont 'A' et 'K'.
L'exemple suivant compare l'aplatissement produit par deux parcours différents, sur un tableau à deux dimensions :
On peut clairement voir la différence entre les deux types de parcours du tableau data, soit « par lignes » ou « par colonnes », sur le résultat de l'exécution :
[1 2 3 4 5 6] [1 4 2 5 3 6]
La figure 7 illustre le parcours du tableau à deux dimensions data suivant l'ordre du langage de programmation C ou de Fortran, c'est-à-dire soit « en lignes » (à gauche) soit « en colonnes » (à droite).
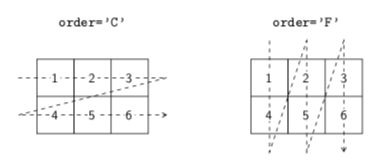
order des fonctions ravel et flatten permet de définir l'ordre dans lequel les éléments sont parcourus lors de la création d'un aplatissement de tableau.Nouvelle dimension
On peut vouloir ajouter une dimension à un tableau déjà existant, sans pour autant modifier sa taille ni les éléments qu'il contient. Pour ce faire, il faut simplement modifier la forme du tableau. On peut donc, par exemple, utiliser la fonction reshape pour ce faire :
On peut voir, sur le résultat de l'exécution, que la forme du tableau créé par reshape est bien de $(1, 4)$ et que celui-ci est donc passé d'une dimension à deux dimensions :
(1, 4) [[0 1 2 3]]
On peut obtenir le même résultat avec l'opérateur de slicing en utilisant une construction particulière se basant sur np.newaxis qui crée un nouvel axe. Voici comment l'exemple précédent se réécrit :
On utilise donc l'opérateur de slicing pour extraire un sous-tableau du tableau data, en précisant deux slices entre les crochets. Comme le tableau ne possède qu'une seule dimension, cela n'a normalement pas de sens. La subtilité est que l'un des deux slices est np.newaxis, ce qui correspond à l'ajout d'un nouvel axe.
Lorsque l'on passe d'une dimension à la dimension supérieure, on a le choix d'où placer le nouvel axe. Voici les deux possibilités que l'on a, en fait, pour l'exemple précédent :
Le tableau unidimensionnel data est devenu un tableau à deux dimensions, soit sous forme d'une « ligne » (dans la variable a), ou alors sous forme d'une « colonne » (dans la variable b) :
(1, 4) (4, 1) [[0 1 2 3]] [[0] [1] [2] [3]]